What are the concept of the fourth-degree identity and some examples thereof? In Vietnam, what is the grade whose Mathematics curriculum covers the identity?

What are the concept of the fourth-degree identity and some examples thereof?

Students can refer to the following information on the fourth-degree identity and some examples thereof:

*Note: The information is for reference only./

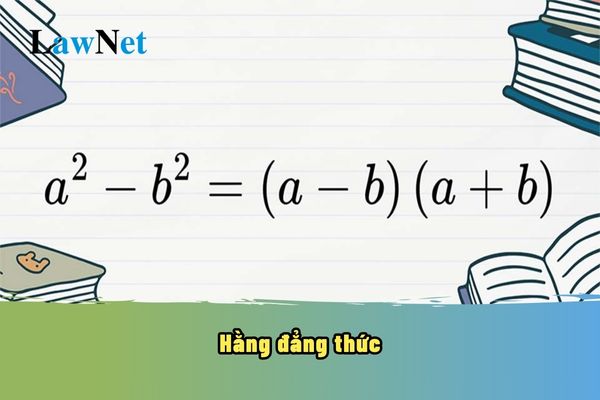
What are the concept of the fourth-degree identity and some examples thereof? In Vietnam, what is the grade whose Mathematics curriculum covers the identity? (Image from the Internet)

In Vietnam, what is the grade whose Mathematics curriculum covers the identity?

Under Section 5 of the Appendix of the General education program in Mathematics issued together with Circular 32/2018/TT-BGDDT on the requirements for the 8th-grade Mathematics curriculum, the 7 notable identities are taught as follows:

The notable identities are part of the algebra section.

To be specific, in the algebraic expression section, the lesson on notable identities must cover the following content:

- Recognize the concepts: identity, identity equation.

- Describe the identities: square of a sum and difference; difference of squares; cube of a sum and difference; sum and difference of cubes.

- Apply the identities to factorize polynomials in the form of: directly applying the identities; applying the identities through grouping terms and factoring out the common factor.

Thus, according to the above regulation, the notable identities are taught in the 8th-grade Mathematics curriculum.

What are the basic teaching methods for Mathematics in Vietnam?

Under Section 6 of the General education program in Mathematics issued together with Circular 32/2018/TT-BGDDT, the Mathematics curricula in general and the 8th-grade Mathematics curriculum in particular will utilize the following methods:

- The teaching method in the Mathematics curriculum must meet the following basic requirements:

+ Being suitable to the cognitive process of students (from concrete to abstract, from easy to difficult); not only focused on the logical structure of mathematical science but also on approaches based on student's experience and learning;

+ Adhering to the spirit of "student-centered learning," enhancing proactiveness, self-awareness, and attention to students' needs, cognitive abilities, and different learning styles of each student; organizing the teaching process in a constructivist approach, where students engage in exploration, discovery, and problem-solving;

+ Flexibly applying various positive teaching methods and techniques; skillfully and creatively combining with traditional teaching methods and techniques; integrating classroom learning activities with experiential learning, applying mathematical knowledge in practice. The lesson structure ensures a balanced, harmonious ratio between core knowledge, applied knowledge, and other components.

+ Utilizing fully and effectively the minimal required teaching tools and equipment according to the regulations for Mathematics; appropriate use of self-made teaching aids suitable for learning content and student groups; increasing the use of information technology and modern teaching tools and equipment in a suitable and effective manner;

- Orientation on methods to form and develop key traits and general capabilities

+ Methods to form and develop key traits

Through organizing learning activities, Mathematics contributes alongside other subjects and educational activities to help students train honesty, a love for labor, responsibility, a sense of completing learning tasks; nurture confidence, an interest in learning, a habit of reading, and a sense of curiosity and scientific exploration.

+ Methods to form and develop general capabilities

++ Mathematics contributes to forming and developing the capacity for self-management and self-learning through training learners to choose goals, make learning plans, develop self-learning methods, review experiences, and make adjustments for application in other situations while learning mathematical concepts, knowledge, and skills, as well as in practicing, training, or independently solving mathematical problems and issues of mathematical significance.

++ Mathematics contributes to forming and developing the capacity for communication and collaboration through listening and understanding, reading and writing, expressing necessary mathematical information in mathematical texts; through effectively using mathematical language combined with ordinary language to discuss and present mathematical contents, ideas, and solutions in interactions with others, while showing confidence and respect to the interlocutor when describing, explaining mathematical content and ideas.

++ Mathematics contributes to forming and developing the capacity for problem-solving and creativity by helping students recognize problematic situations; sharing understanding of the problem with others; determining, choosing a solution and presenting the solution for the problem; evaluating the implemented solution and generalizing it for similar issues.

- The teaching method of Mathematics contributes to forming and developing numeracy skills, language skills, and other specific skills. To be specific:

+ With its outstanding features, Mathematics has many opportunities to develop numeracy skills, demonstrated by providing mathematical knowledge, training calculation skills, and estimation, while helping to form and develop components of mathematical abilities (thinking and reasoning skills, modeling skills, problem-solving skills; communication skills, and the ability to use tools and media in learning math).

+ Mathematics contributes to the development of language skills through practicing reading comprehension, explanation, analysis, and evaluation of mathematically meaningful situations, through effectively using mathematical language combined with ordinary language to present and express mathematical content, ideas, and solutions.

+ Mathematics contributes to developing computer skills by using information technology and communication tools as support tools in learning and self-study; creating a learning environment for applied experience.

+ Mathematics contributes to the development of aesthetic appreciation through helping students become familiar with the history of mathematics, with the biographies of mathematicians and through recognizing the beauty of Mathematics in the natural world.

Download the General education program in Mathematics issued together with Circular 32/2018/TT-BGDDT.