What are the guidelines for proving two triangles are similar? What is the grade whose Mathematics curriculum covers the content on similar triangles in Vietnam?

What are the guidelines for proving two triangles are similar?

Two triangles are considered similar if they have the same shape but not necessarily the same size, meaning their corresponding angles are equal, and their corresponding sides are proportional. To prove two triangles are similar, we rely on theorems and similarity properties in geometry.

Students can refer to the following guidelines for proving two triangles are similar and illustrative exercises:

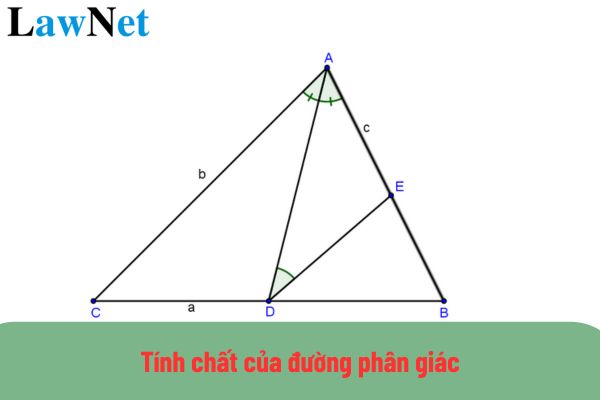
A. Cases of Similar Triangles 1. Case of Similarity 1: Two triangles have corresponding sides proportional to each other (side - side - side) Consider triangles ∆ABC and ∆DEF, we have the ratios: AB/DE = BC/EF = AC/DF => We can conclude: ∆ABC ~ ∆DEF (s - s - s) 2. Case of Similarity 2: Two triangles have two corresponding sides proportional to each other and the angle between these sides is equal (side - angle - side) Consider ∆ABC and ∆DEF, we have the ratios: AB/DE = AC/DF Angle BAC = Angle EDF => We can conclude: ∆ABC ~ ∆DEF (s - a - s) 3. Case of Similarity 3: Two triangles have two corresponding angles equal (angle - angle) Consider ∆ABC and ∆DEF, we have: Angle ABC = Angle DEF Angle BAC = Angle EDF => ∆ABC ~ ∆DEF (a - a) B. Similarity Theorems for Right Triangles 1. Theorem for Two Right Triangles 1: (hypotenuse - leg) If two right triangles satisfy the condition: the hypotenuse and a leg of one triangle are proportional to the hypotenuse and a leg of the other triangle, then these right triangles are similar. 2. Theorem for Two Right Triangles 2: (two legs) If the two legs of one triangle are respectively proportional to the two legs of the other triangle, then the right triangles are similar. 3. Theorem for Three Right Triangles 3: (angle) If one of the two acute angles of one triangle equals one of the two acute angles of the other triangle, then the right triangles are similar. C. Several Forms and Methods to Prove Triangle Similarity Form 1: Method to Prove Two Triangles Similar - Using Ratios: Exercise: Given ∆ABC (condition AB < AC), line segment AD is an internal bisector. In the external region of ∆ABC, draw ray Cx such that Angle BCx = Angle BAD. Let point I be the intersection of line Cx and the line through points A, D. Prove that: a) Prove triangles: ∆ADB is similar to ∆CDI. b) Prove that: AD/AC = AB/AI c) Prove that AD² = AB.AC – BD.DC 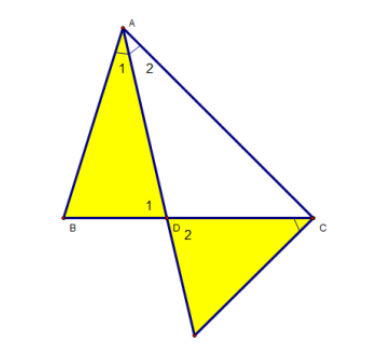Solution Guide a) Consider triangles ∆ADB and ∆CDI, we have: Angle BCx = Angle BAD (according to hypothesis) Angle D1 = Angle D2 (vertically opposite) => ∆ADB ~ ∆CDI b) Consider triangles ∆ABD and ∆AIC, we have: Angle B = Angle I (since ∆ADB is similar to triangle ∆CDI) Angle A1 = Angle A2 (AD is a bisector) => We have: ∆ABD ~ ∆AIC => Therefore, ratio AD/AC = AB/AI c) From the result of part b, we have: AD.AI = AB.AC (1) We have: ∆ADB ~ ∆CDI => AD.DI = BD.CD (2) From result (1) and (2): AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI) = AD.AD = AD² Therefore, AD² = AB.AC – BD.CD Form 2: How to Prove Two Triangles Similar - Thales's Theorem + Two Parallel Lines Problem: Given ∆ABC as an acute triangle. Draw two altitudes from vertices B and C, noted as BD and CE, respectively. Subsequently, draw altitudes DF and EG of ∆ADE. Requirements: a) Prove that ∆ABD ~ ∆AEG. b) Prove that AD.AE = AB.AG = AC.AF c) Prove that FG // BC Solution Guide a) Consider ∆ABD and ∆AEG, we have: BD ⊥ AC (BD is an altitude) EG ⊥ AC (EG is an altitude) => BD // EG => ∆ABD ~ ∆AGE b) We have AB/AE = AD/AG => AD.AE = AB.AG (1) Proven similarly, we get: AD.AE = AC.AF (2) From data (1) and (2), we deduce: AD.AE = AB.AG = AC.AF c) Consider ∆ABC, we have: AB.AG = AC.AF (proven in part b) => FG // BC (according to converse of Thales's theorem) Form 3: Method to Prove Two Triangles Similar - Equal Corresponding Angles Problem: Given ∆ABC, where altitudes BD and CE intersect at H. Requirements: a) Prove that ∆HBE is similar to ∆HCE. b) Prove that ∆HED is similar to ∆HBC and angle HDE = angle HAE c) Knowing BD = CD. Let point M be the intersection of AH and BC. Prove that DE ⊥ EM. 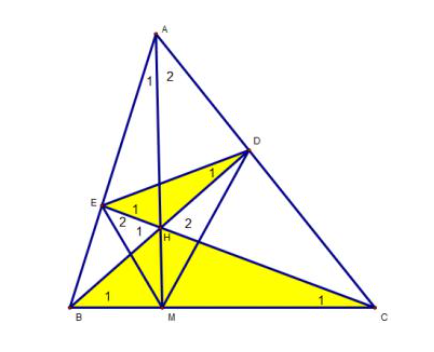Solution Guide a) Consider two ∆HBE and ∆HCD, we have: Angle BEH = Angle CDG = 90 degrees (According to hypothesis) Angle H1 = Angle H2 (vertically opposite) Therefore, we have ∆HBE ~ ∆HCD (according to property a - a) b) For ∆HED and ∆HBC, we have: HE/HD = HB/HC (since ∆HBE ~ ∆HCD) => HE/HB = HD/HC And we have angle EHD = angle CHB (vertically opposite) => Triangle ∆HED ~ ∆HBC (due to property s - a - s) => Angle D1 = angle C1 (1) Moreover: Altitudes BD and CE intersect at H (according to hypothesis) => Point H is the orthocenter. => AH ⊥ BC at M. => angle A1 + angle ABC = 90 degrees Moreover, we have: angle C1 + angle ABC = 90 degrees (2) => From data (1) and (2), we have: angle A1 = D1 or: angle HDE = angle HAE c) Proven similarly to part b, we have: angle A2 = E2 (3) Consider ∆BCD, we have: DB = DC (according to hypothesis) => ∆BCD is an isosceles triangle at D => angle B1 = angle ACB Moreover: angle B1 = angle E1 (since ∆HED ~ ∆HBC) => Angle E1 = angle ACB Moreover: angle A2 + angle ACB = 90 degrees Angle A2 = angle E2 (proven above) => Angle E1 + angle E2 = 90 degrees or angle DEM = 90 degrees => ED is perpendicular to EM.

Note: The content  is for reference purposes only.

What are the guidelines for proving two triangles are similar? What is the grade whose Mathematics curriculum covers the content on similar triangles in Vietnam? (Image from the Internet)

What is the grade whose Mathematics curriculum covers the content on similar triangles in Vietnam?

Under Section 5 of the General education program in Mathematics issued together with Circular 32/2018/TT-BGDDT,  the educational content for 8th-grade students is as follows:

Plane Geometry

...

Similar Shapes

Similar Triangles

- Able to describe the definition of two similar triangles.

- Explain cases of similarity for two triangles, and for two right triangles.

- Solve practical problems related to the application of knowledge about two similar triangles (e.g., calculating the height dropped to the hypotenuse in a right triangle by using the relation between that height and the product of the two projections of the legs onto the hypotenuse; indirect measurement of an object's height; calculate the distance between two places with one place being inaccessible,...).

...

Thus, the content on similar triangles first appears in the 8th-grade Mathematics Curriculum

What are the forms of periodic assessment for 8th-grade students in Vietnam?

Under Clause 1, Article 7 of Circular 22/2021/TT-BGDDT, the forms of periodic assessment for 8th-grade students in Vietnam include: examination (on test paper or on computer), practice exercises, or learning projects.

- Time of examination (on test paper or on computer) of subjects (excluding learning topics) with up to 70 periods/school year is 45 minutes; time of examination (on test paper or on computer) of subjects (excluding learning topics with more than 70 periods/school year is from 60 minutes to 90 minutes or up to 120 minutes for specialized subjects.

- For examination (on test paper or on computer) where assessment is made via scores, exam questions are developed based on exam mechanisms and characteristics in a manner that satisfies requirements of the subjects under formal education program.

- For examination (on test paper or on computer) where assessment is conducted via feedback, practice exercises, or learning projects, provide instructions and assessment criteria based on requirements of subjects under formal education program prior to implementation.