Cách chứng minh hai tam giác đồng dạng? Nội dung tam giác đồng dạng được học ở lớp mấy?
Cách chứng minh hai tam giác đồng dạng?
Hai tam giác được coi là đồng dạng nếu chúng có cùng hình dạng nhưng không nhất thiết phải cùng kích thước, tức là các góc tương ứng bằng nhau và các cạnh tương ứng tỷ lệ. Để chứng minh hai tam giác đồng dạng, chúng ta cần dựa vào các định lý và tính chất đồng dạng trong hình học.
Dưới đây là hướng dẫn cách chứng minh hai tam giác đồng dạng và bài tập minh họa mà học sinh có thể tham khảo.
A. Các trường hợp tam giác đồng dạng 1. Trường hợp đồng dạng số 1: 2 tam giác có 3 cạnh tương ứng tỉ lệ với nhau (cạnh – cạnh – cạnh) Xét 2 tam giác ∆ABC và ∆DEF, ta có các tỉ số: AB/DE = BC/EF = AC/DF => Ta có thể kết luận: ∆ABC ~ ∆DEF (c – c – c) 2. Trường hợp đồng dạng số 2: 2 tam giác có 2 cạnh tương ứng tỉ lệ với nhau – góc xen giữa hai cạnh bằng nhau (cạnh – góc – cạnh) Xét ∆ABC và ∆DEF, ta có các tỉ số: AB/DE = AC/DF Góc BAC = góc EDF => Ta có thể kết luận: ∆ABC ~ ∆DEF (c – g – c) 3. Trường hợp đồng dạng số 3: 2 tam giác có hai góc tương ứng bằng nhau (góc – góc) Xét ∆ABC và ∆DEF, ta có : Góc ABC = Góc DEF Góc BAC = Góc EDF => ∆ABC ~ ∆DEF (g – g) B. Các định lí đồng dạng của hai tam giác vuông 1. Định lí của 2 tam giác vuông số 1: (cạnh huyền – cạnh góc vuông) Nếu 2 tam giác vuông thỏa mãn điều kiện: cạnh huyền và cạnh góc vuông của tam giác này có cùng tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác kia thì hai tam giác vuông này đồng dạng với nhau. 2. Định lí của 2 tam giác vuông số 2: (hai cạnh góc vuông) Nếu hai cạnh góc vuông của tam giác này lần lượt có cùng tỉ lệ với hai cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng với nhau. 3. Định lí của 3 tam giác vuông số 3: (góc) Nếu một trong 2 góc nhọn của tam giác này bằng một trong 2 góc nhọn của tam giác kia thì 2 tam giác vuông đó đồng dạng với nhau. C. Một số dạng bài và phương pháp chứng minh tam giác đồng dạng Dạng 1: Phương pháp chứng minh 2 tam giác đồng dạng – Sử dụng hệ thức: Bài tập: Cho ∆ABC (điều kiện độ dài cạnh AB < AC), có đoạn thẳng AD là đường phân giác trong. Tại miền ngoài ∆ABC ta góc BCx = góc BAD vẽ tia Cx sao cho . Gọi điểm I là giao điểm của đường thẳng Cx và đường thẳng đi qua 2 điểm A, D. Chứng minh rằng: a) Chứng minh 2 tam giác: ∆ADB đồng dạng ∆CDI. b) Chứng minh rằng: AD/AC = AB/AI c) Chứng minh rằng AD² = AB.AC – BD.DC
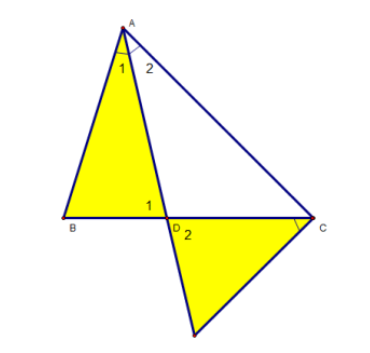
Hướng dẫn giải a) Xét 2 tam giác ∆ADB và ∆CDI, ta có: Góc BCx = góc BAD (theo giả thuyết) Góc D1 = Góc D2 (đối đỉnh) => ∆ADB ~ ∆CDI b) Xét 2 tam giác ∆ABD và ∆AIC, ta có: Góc B = Góc I (do ∆ADB đồng dạng với tam giác ∆CDI) Góc A1 = góc A2 (AD là phân giác) => Ta có: ∆ABD ~ ∆AIC => Vậy tỉ số AD/AC = AB/AI c) Từ kết quả của câu b ta có: AD.AI = AB.AC (1) Ta có: ∆ADB ~ ∆CDI => ta có AD.DI = BD.CD (2) Từ hệ quả (1) và (2) : AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI ) = AD.AD = AD² Vậy AD² = AB.AC – BD.CD Dạng 2: Cách chứng minh hai tam giác đồng dạng – Định lí Talet + hai đường thẳng song song Bài toán: Cho ∆ABC là tam giác nhọn. Vẽ 2 đường cao được vẽ từ các đỉnh B và C lần lượt là BD và CE. Lần lượt vẽ các đường cao DF và EG của ∆ADE. Yêu cầu: a) Hãy chứng minh rằng ∆ABD ~ ∆AEG. b) Hãy chứng minh rằng AD.AE = AB.AG = AC.AF c) Hãy chứng minh rằng FG // BC Hướng dẫn giải a) Xét ∆ABD và ∆AEG, ta có : BD AC (BD là đường cao) EG AC (EG là đường cao) => BD // EG => ∆ABD ~ ∆AGE b) Ta có AB/AE = AD/AG => AD.AE = AB.AG (1) Chứng minh tương tự, ta được : AD.AE = AC.AF (2) Từ dữ kiện (1) và (2) ta suy ra : AD.AE = AB.AG = AC.AF c) Xét ∆ABC, ta có : AB.AG = AC.AF (chứng minh theo câu b) => FG // BC (theo định lí đảo talet) Dạng 3: Phương pháp chứng minh hai tam giác đồng dạng – góc tương ứng bằng nhau Bài toán: Cho ∆ABC có các đường cao BD và CE cắt nhau tại H. Yêu cầu: a) Chứng minh rằng ∆HBE đồng dạng ∆HCE. b) Chứng minh rằng ∆HED đồng dạng ∆HBC và góc HDE = góc HAE c) Biết rằng BD = CD. Gọi điểm M là giao điểm của AH và BC. Chứng minh rằng: DE vuông góc EM.
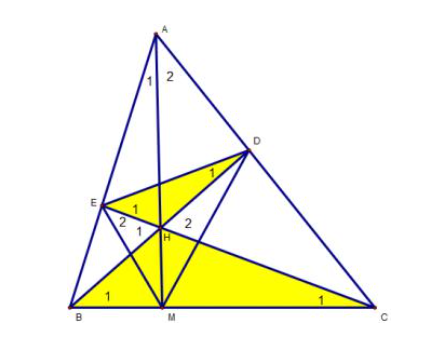
Hướng dẫn giải a) Xét 2 ∆HBE và ∆HCD ta có : Góc BEH = góc CDG = 90 độ (Theo giả thuyết) Góc H1 = góc H2 (đối đỉnh) Suy ra ta có ∆HBE ~ ∆HCD (theo tính chất g – g) b) ∆HED và ∆HBC, ta có : HE/HD = HB/HC (do ∆HBE ~ ∆HCD) => HE/HB = HD/HC Mà ta có góc EHD = góc CHB (đối đỉnh) => Tam giác ∆HED ~ ∆HBC (do tính chất c – g – c) => Góc D1 = góc C1 (1) mà: Đường cao BD và CE cắt nhau tại H (theo giả thuyết) => Điểm H là điểm trực tâm. => AH vuông góc BC tại M. => góc A1 + góc ABC = 90 độ mặt khác ta có: góc C1 + góc ABC = 90 độ (2) => Từ dữ kiện (1) và (2) ta có: góc A1 = D1 hay: góc HDE = góc HAE c) Chứng minh tương tự câu b, ta có: góc A2 = E2 (3) xét ∆BCD, ta có : DB = DC (theo giả thuyết) => ∆BCD là tam giác cân tại D => góc B1 = góc ACB mà: góc B1 = góc E1 (do ∆HED ~ ∆HBC) => Góc E1 = góc ACB mà: góc A2 + góc ACB = 90 độ Góc A2 = góc E2 (chứng minh trên) => Góc E1 + góc E2 = 90 độ hay góc DEM = 90 độ => ED vuông góc với EM. |
Lưu ý: Nội dung Cách chứng minh hai tam giác đồng dạng? chỉ mang tính chất tham khảo.

Cách chứng minh hai tam giác đồng dạng? Nội dung tam giác đồng dạng được học ở lớp mấy? (Hình từ Internet)
Nội dung tam giác đồng dạng được học ở lớp mấy?
Căn cứ Mục 5 Chương trình giáo dục phổ thông môn Toán ban hành kèm theo Thông tư 32/2018/TT-BGDĐT quy định về nội dung giáo dục của học sinh lớp 8 như sau:
Hình học phẳng
...
Hình đồng dạng
Tam giác đồng dạng
- Mô tả được định nghĩa của hai tam giác đồng dạng.
- Giải thích được các trường hợp đồng dạng của hai tam giác, của hai tam giác vuông.
- Giải quyết được một số vấn đề thực tiễn gắn với việc vận dụng kiến thức về hai tam giác đồng dạng (ví dụ: tính độ dài đường cao hạ xuống cạnh huyền trong tam giác vuông bằng cách sử dụng mối quan hệ giữa đường cao đó với tích của hai hình chiếu của hai cạnh góc vuông lên cạnh huyền; đo gián tiếp chiều cao của vật; tính khoảng cách giữa hai vị trí trong đó có một vị trí không thể tới được,...).
...
Như vậy, xuyên suốt Chương trình giáo dục phổ thông môn Toán của 12 khối lớp, nội dung tam giác đồng dạng xuất hiện đầu tiên trong nội dung lớp 8. Do đó, tam giác đồng dạng sẽ được học bắt đầu từ học sinh lớp 8.
Hình thức đánh giá định kì đối với học sinh lớp 8 là gì?
Căn cứ khoản 1 Điều 7 Thông tư 22/2021/TT-BGDĐT quy định hình thức đánh giá định kì đối với học sinh lớp 8 bao gồm: bài kiểm tra (trên giấy hoặc trên máy tính), bài thực hành, dự án học tập.
- Thời gian làm bài kiểm tra (trên giấy hoặc trên máy tính) đối với môn học (không bao gồm cụm chuyên đề học tập) có từ 70 tiết/năm học trở xuống là 45 phút, đối với môn học (không bao gồm cụm chuyên đề học tập) có trên 70 tiết/năm học từ 60 phút đến 90 phút; đối với môn chuyên tối đa 120 phút.
- Đối với bài kiểm tra (trên giấy hoặc trên máy tính) đánh giá bằng điểm số, đề kiểm tra được xây dựng dựa trên ma trận, đặc tả của đề kiểm tra, đáp ứng theo yêu cầu cần đạt của môn học được quy định trong Chương trình giáo dục phổ thông.
- Đối với bài kiểm tra (trên giấy hoặc trên máy tính) đánh giá bằng nhận xét, bài thực hành, dự án học tập, phải có hướng dẫn và tiêu chí đánh giá theo yêu cầu cần đạt của môn học được quy định trong Chương trình giáo dục phổ thông trước khi thực hiện.








- Điều kiện giáo viên nước ngoài dạy ngoại ngữ trong trường mầm non?
- Hướng dẫn xử lý khi xảy ra bạo lực học đường?
- Vì sao nói Công xã Paris là nhà nước kiểu mới? Lớp học Lịch sử của học sinh lớp 8 được tổ chức thế nào?
- Mẫu văn tả chú bộ đội lớp 5 ngắn gọn hay nhất? Hoạt động trải nghiệm cấp tiểu học lớp 5 như thế nào?
- Top các mẫu đoạn văn về một nhân vật em yêu thích trong câu chuyện đã đọc, đã nghe? Học sinh lớp 3 được quyền chọn trường học không?
- Top 10 Mẫu viết đoạn văn về một cảnh đẹp thiên nhiên trong đó có sử dụng biện pháp tu từ so sánh hoặc ẩn dụ hay nhất?
- Mẫu viết đoạn văn khoảng 200 chữ ghi lại cảm xúc về bài thơ Mẹ môn Ngữ văn lớp 7? Việc đánh giá học sinh lớp 7 có mục đích là gì?
- Trọn bộ đề thi cuối kì 1 Văn 11 kèm đáp án? Trường THPT chuyên được ưu tiên những gì để bảo đảm chất lượng giáo dục?
- Công dân học tập vn đăng nhập hướng dẫn chi tiết? Kinh phí thực hiện xây dựng mô hình Công dân học tập giai đoạn 2021 2030?
- Mẫu Kịch bản tổ chức lễ Noel cho trẻ mầm non? Các loại hình của cơ sở giáo dục mầm non hiện nay?