Công thức Cos là gì? Một vài ví dụ áp dụng công thức Cos? Công thức Cos sẽ được học ở lớp mấy?
Công thức Cos là gì? Một vài ví dụ áp dụng công thức Cos?
Công thức cosin là một công cụ hữu ích trong việc giải các bài toán liên quan đến tam giác. Việc nắm vững công thức này sẽ giúp bạn giải quyết các bài toán hình học một cách nhanh chóng và chính xác hơn.
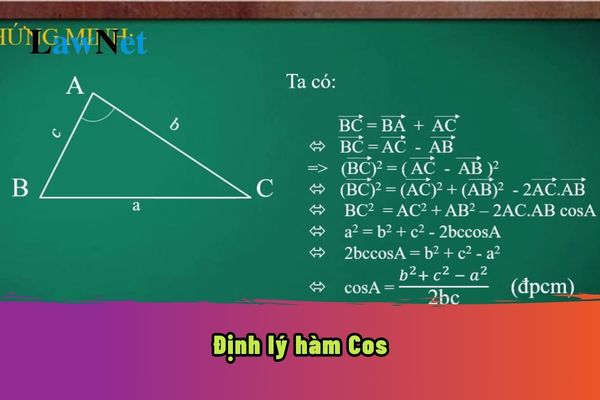
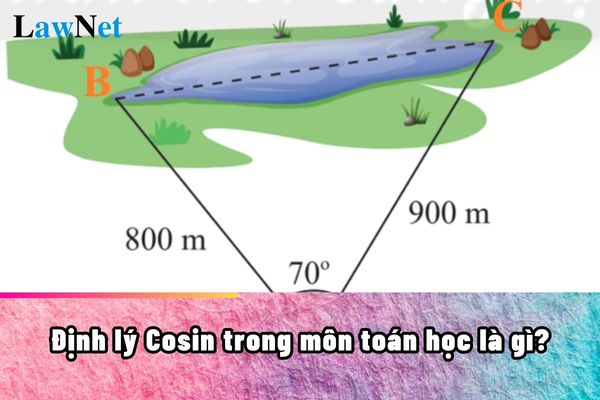
Trong hình học, công thức cosin là một mối liên hệ giữa các cạnh của một tam giác. Nó cho phép ta tính độ dài một cạnh của tam giác khi biết độ dài hai cạnh còn lại và góc xen giữa. *Công thức tổng quát: c² = a² + b² - 2ab * cos(C) Trong đó: c: Là độ dài cạnh đối diện với góc C a, b: Là độ dài hai cạnh còn lại C: Là góc xen giữa hai cạnh a và b *Ứng dụng của công thức Cosin Công thức cosin có rất nhiều ứng dụng trong việc giải các bài toán hình học, đặc biệt là trong các trường hợp: Tính độ dài cạnh của tam giác: Khi biết hai cạnh và góc xen giữa. Tính góc của tam giác: Khi biết ba cạnh của tam giác. Giải các bài toán liên quan đến tam giác: Như tính diện tích tam giác, chứng minh các tính chất hình học,... Ví dụ 1: Cho tam giác ABC có AB = 5cm, AC = 7cm và góc BAC = 60 độ. Tính độ dài cạnh BC. Giải: Áp dụng công thức cosin, ta có: BC² = AB² + AC² - 2 * AB * AC * cos(BAC) BC² = 5² + 7² - 2 * 5 * 7 * cos(60) BC² = 25 + 49 - 35 BC² = 39 BC ≈ 6.24 cm Vậy độ dài cạnh BC xấp xỉ 6.24 cm. Ví dụ 2: Cho tam giác ABC có AB = 6cm, BC = 8cm và AC = 10cm. Tính góc BAC. Giải: Áp dụng công thức cosin, ta có: 10² = 6² + 8² - 2 * 6 * 8 * cos(BAC) cos(BAC) = (6² + 8² - 10²) / (2 * 6 * 8) cos(BAC) = 1/4 BAC ≈ 75.52° Vậy góc BAC xấp xỉ 75.52 độ. |
*Lưu ý: Thông tin về Công thức Cos là gì? Một vài ví dụ áp dụng công thức Cos? chỉ mang tính chất tham khảo./.
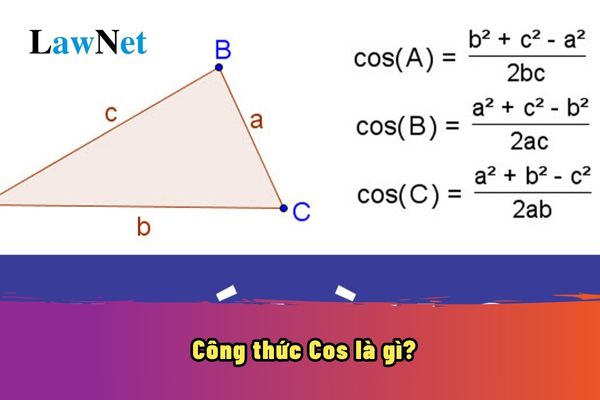
Công thức Cos là gì? Một vài ví dụ áp dụng công thức Cos? Công thức Cos sẽ được học ở lớp mấy? (Hình từ Internet)
Công thức Cos sẽ được học ở lớp mấy?
Căn cứ theo Mục 5 Chương trình giáo dục phổ thông môn toán ban hành kèm theo Thông tư 32/2018/TT-BGDĐT nội dung trong môn Toán lớp 9 như sau:
*Hệ thức lượng trong tam giác vuông
Tỉ số lượng giác của góc nhọn. Một số hệ thức về cạnh và góc trong tam giác vuông
- Nhận biết được các giá trị sin (sine), côsin (cosine), tang (tangent), côtang (cotangent) của góc nhọn.
- Giải thích được tỉ số lượng giác của các góc nhọn đặc biệt (góc 30o, 45o, 60o) và của hai góc phụ nhau.
- Tính được giá trị (đúng hoặc gần đúng) tỉ số lượng giác của góc nhọn bằng máy tính cầm tay.
- Giải thích được một số hệ thức về cạnh và góc trong tam giác vuông (cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề; cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề).
- Giải quyết được một số vấn đề thực tiễn gắn với tỉ số lượng giác của góc nhọn (ví dụ: Tính độ dài đoạn thẳng, độ lớn góc và áp dụng giải tam giác vuông,...).
Như vậy, đối chiếu quy định trên thì công thức Cos sẽ được học ở lớp 9.
Quy định về việc đánh giá kết quả giáo dục môn Toán lớp 9 như thế nào?
Căn cứ theo Mục 7 Chương trình giáo dục phổ thông môn toán ban hành kèm theo Thông tư 32/2018/TT-BGDĐT thì việc đánh giá kết quả giáo dục nói chung hay đánh giá kết quả giáo dục trong môn Toán lớp 9 như sau:
Mục tiêu đánh giá kết quả giáo dục môn Toán là cung cấp thông tin chính xác, kịp thời, có giá trị về sự phát triển năng lực và sự tiến bộ của học sinh trên cơ sở yêu cầu cần đạt ở mỗi lớp học, cấp học; điều chỉnh các hoạt động dạy học, bảo đảm sự tiến bộ của từng học sinh và nâng cao chất lượng giáo dục môn Toán nói riêng và chất lượng giáo dục nói chung.
Vận dụng kết hợp nhiều hình thức đánh giá (đánh giá quá trình, đánh giá định kì), nhiều phương pháp đánh giá (quan sát, ghi lại quá trình thực hiện, vấn đáp, trắc nghiệm khách quan, tự luận, kiểm tra viết, bài tập thực hành, các dự án/sản phẩm học tập, thực hiện nhiệm vụ thực tiễn,...) và vào những thời điểm thích hợp.
Đánh giá quá trình (hay đánh giá thường xuyên) do giáo viên phụ trách môn học tổ chức, kết hợp với đánh giá của giáo viên các môn học khác, của bản thân học sinh được đánh giá và của các học sinh khác trong tổ, trong lớp hoặc đánh giá của cha mẹ học sinh. Đánh giá quá trình đi liền với tiến trình hoạt động học tập của học sinh, tránh tình trạng tách rời giữa quá trình dạy học và quá trình đánh giá, bảo đảm mục tiêu đánh giá vì sự tiến bộ trong học tập của học sinh.
Đánh giá định kì (hay đánh giá tổng kết) có mục đích chính là đánh giá việc thực hiện các mục tiêu học tập. Kết quả đánh giá định kì và đánh giá tổng kết được sử dụng để chứng nhận cấp độ học tập, công nhận thành tích của học sinh. Đánh giá định kì do cơ sở giáo dục tổ chức hoặc thông qua các kì kiểm tra, đánh giá quốc gia.
Đánh giá định kì còn được sử dụng để phục vụ quản lí các hoạt động dạy học, bảo đảm chất lượng ở cơ sở giáo dục và phục vụ phát triển chương trình môn Toán.
Đánh giá năng lực học sinh thông qua các bằng chứng biểu hiện kết quả đạt được trong quá trình thực hiện các hành động của học sinh. Tiến trình đánh giá gồm các bước cơ bản như: xác định mục đích đánh giá; xác định bằng chứng cần thiết; lựa chọn các phương pháp, công cụ đánh giá thích hợp; thu thập bằng chứng; giải thích bằng chứng và đưa ra nhận xét.
Chú trọng việc lựa chọn phương pháp, công cụ đánh giá các thành tố của năng lực toán học. Cụ thể:
- Đánh giá năng lực tư duy và lập luận toán học: có thể sử dụng một số phương pháp, công cụ đánh giá như các câu hỏi (nói, viết), bài tập,... mà đòi hỏi học sinh phải trình bày, so sánh, phân tích, tổng hợp, hệ thống hoá kiến thức; phải vận dụng kiến thức toán học để giải thích, lập luận.
- Đánh giá năng lực mô hình hoá toán học: lựa chọn những tình huống trong thực tiễn làm xuất hiện bài toán toán học. Từ đó, đòi hỏi học sinh phải xác định được mô hình toán học (gồm công thức, phương trình, bảng biểu, đồ thị,...) cho tình huống xuất hiện trong bài toán thực tiễn; giải quyết được những vấn đề toán học trong mô hình được thiết lập; thể hiện và đánh giá được lời giải trong ngữ cảnh thực tiễn và cải tiến được mô hình nếu cách giải quyết không phù hợp.
- Đánh giá năng lực giải quyết vấn đề toán học:
+ Có thể sử dụng các phương pháp như yêu cầu người học nhận dạng tình huống, phát hiện và trình bày vấn đề cần giải quyết; mô tả, giải thích các thông tin ban đầu, mục tiêu, mong muốn của tình huống vấn đề đang xem xét;
+ Thu thập, lựa chọn, sắp xếp thông tin và kết nối với kiến thức đã có; sử dụng các câu hỏi (có thể yêu cầu trả lời nói hoặc viết) đòi hỏi người học vận dụng kiến thức vào giải quyết vấn đề, đặc biệt các vấn đề thực tiễn; sử dụng phương pháp quan sát, quan sát người học trong quá trình giải quyết vấn đề; đánh giá qua các sản phẩm thực hành của người học; quan tâm hợp lí đến các nhiệm vụ đánh giá mang tính tích hợp.
- Đánh giá năng lực giao tiếp toán học: có thể sử dụng các phương pháp như yêu cầu người học nghe hiểu, đọc hiểu, ghi chép (tóm tắt), phân tích, lựa chọn, trích xuất được được các thông tin toán học cơ bản, trọng tâm trong văn bản nói hoặc viết; sử dụng được ngôn ngữ toán học kết hợp với ngôn ngữ thông thường trong việc trình bày, diễn đạt, nêu câu hỏi, thảo luận, tranh luận các nội dung, ý tưởng, giải pháp toán học trong sự tương tác với người khác.
- Đánh giá năng lực sử dụng công cụ, phương tiện học toán: có thể sử dụng các phương pháp như yêu cầu người học nhận biết được tên gọi, tác dụng, quy cách sử dụng, cách thức bảo quản, ưu điểm, hạn chế của các công cụ, phương tiện học toán; trình bày được cách sử dụng (hợp lí) công cụ, phương tiện học toán để thực hiện nhiệm vụ học tập hoặc để diễn tả những lập luận, chứng minh toán học.
Khi giáo viên lên kế hoạch bài học, cần thiết lập các tiêu chí và cách thức đánh giá để bảo đảm ở cuối mỗi bài học học sinh đạt được các yêu cầu cơ bản dựa trên các tiêu chí đã nêu, trước khi thực hiện các hoạt động học tập tiếp theo.
>> Xem Chương trình giáo dục phổ thông môn Toán ban hành kèm theo Thông tư 32/2018/TT-BGDĐT: Tải






- Top 10 Mẫu viết đoạn văn về một cảnh đẹp thiên nhiên trong đó có sử dụng biện pháp tu từ so sánh hoặc ẩn dụ hay nhất?
- Mẫu viết đoạn văn khoảng 200 chữ ghi lại cảm xúc về bài thơ Mẹ môn Ngữ văn lớp 7? Việc đánh giá học sinh lớp 7 có mục đích là gì?
- Trọn bộ đề thi cuối kì 1 Văn 11 kèm đáp án? Trường THPT chuyên được ưu tiên những gì để bảo đảm chất lượng giáo dục?
- Công dân học tập vn đăng nhập hướng dẫn chi tiết? Kinh phí thực hiện xây dựng mô hình Công dân học tập giai đoạn 2021 2030?
- Mẫu Kịch bản tổ chức lễ Noel cho trẻ mầm non? Các loại hình của cơ sở giáo dục mầm non hiện nay?
- Tổng hợp đề thi cuối kì 1 môn Khoa học tự nhiên lớp 8 có đáp án? Hội đồng kỷ luật học sinh trong trường trung học cơ sở gồm những ai?
- Chi tiết đề thi cuối kì 1 môn Lịch sử và Địa lí lớp 8 có đi kèm đáp án? Mục tiêu xây dựng chương trình môn Lịch sử và Địa lí cấp THCS là gì?
- Top 3 bộ đề thi cuối kì 1 môn Ngữ văn lớp 9 đi kèm đáp án? Học sinh lớp 9 được công nhận tốt nghiệp THCS thì cần đáp ứng những điều kiện gì?
- Top mẫu viết đoạn kết thúc khác cho một câu chuyện đã đọc, đã nghe lớp 4? Học sinh tiểu học hay còn gọi là học sinh cấp mấy?
- Mẫu đề thi học kì 1 lớp 6 Tiếng Anh mới nhất? Học sinh trung học cơ sở học trong bao nhiêu năm?

