Tính chất của đường phân giác là gì? Tính chất của đường phân giác được học ở lớp mấy?
Tính chất của đường phân giác là gì?
Đường phân giác của một góc trong tam giác có tính chất chia góc đó thành hai phần bằng nhau và đồng thời chia cạnh đối diện với góc đó theo tỉ lệ với các cạnh kề của góc.
Tính chất của đường phân giác là gì? Tính chất quan trọng nhất của đường phân giác: Tính chất: Mọi điểm nằm trên đường phân giác của một góc thì cách đều hai cạnh của góc đó. Các tính chất khác liên quan: Trong tam giác:Mỗi góc của tam giác có một và chỉ một đường phân giác. Ba đường phân giác của tam giác đồng quy tại một điểm gọi là tâm đường tròn nội tiếp tam giác. Trong tứ giác:Tứ giác nội tiếp đường tròn có các đường phân giác của các góc đối diện vuông góc với nhau. Ứng dụng: Hình học: Đường phân giác được sử dụng rộng rãi trong các bài toán về tam giác, tứ giác, đường tròn. Kiến trúc: Đường phân giác được ứng dụng trong việc thiết kế các công trình kiến trúc, đảm bảo tính cân đối và hài hòa. Ví dụ: Để chia một mảnh đất hình tam giác thành hai phần có diện tích bằng nhau, người ta thường vẽ đường phân giác của một góc của tam giác. Trong thiết kế nội thất, đường phân giác được sử dụng để chia không gian một cách hợp lý và cân đối. Tóm lại: Đường phân giác là một khái niệm quan trọng trong hình học, có nhiều tính chất và ứng dụng đa dạng. Việc hiểu rõ về đường phân giác sẽ giúp bạn giải quyết tốt hơn các bài toán hình học và các vấn đề liên quan đến không gian. |
*Lưu ý: Thông tin về tính chất của đường phân giác chỉ mang tính chất tham khảo./.
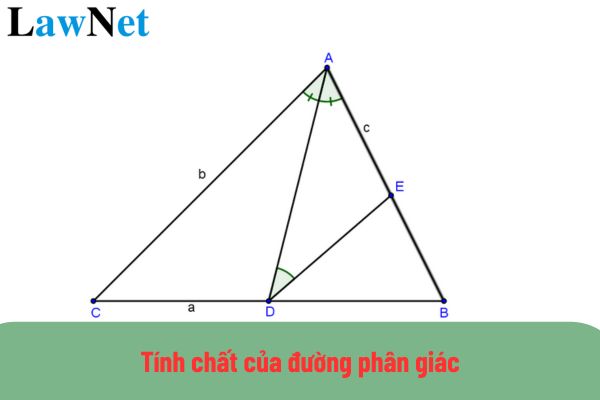
Tính chất của đường phân giác là gì? Tính chất của đường phân giác được học ở lớp mấy? (Hình từ Internet)
Tính chất của đường phân giác được học ở lớp mấy?
Căn cứ theo Mục IV Phụ lục Chương trình giáo dục phổ thông môn Toán ban hành kèm theo Thông tư 32/2018/TT-BGDĐT quy định về yêu cầu cần đạt trong chương trình môn toán lớp 8 như sau:
Yều cầu cần đạt
- Giải thích được định lí Thalès trong tam giác (định lí thuận và đảo).
- Mô tả được định nghĩa đường trung bình của tam giác. Giải thích được tính chất đường trung bình của tam giác (đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó).
- Giải thích được tính chất đường phân giác trong của tam giác.
- Tính được độ dài đoạn thẳng bằng cách sử dụng định lí Thalès.
- Giải quyết được một số vấn đề thực tiễn gắn với việc vận dụng định lí Thalès (ví dụ: tính khoảng cách giữa hai vị trí).
- Mô tả được định nghĩa của hai tam giác đồng dạng.
- Giải thích được các trường hợp đồng dạng của hai tam giác, của hai tam giác vuông.
- Giải quyết được một số vấn đề thực tiễn gắn với việc vận dụng kiến thức về hai tam giác đồng dạng (ví dụ: tính độ dài đường cao hạ xuống cạnh huyền trong tam giác vuông bằng cách sử dụng mối quan hệ giữa đường cao đó với tích của hai hình chiếu của hai cạnh góc vuông lên cạnh huyền; đo gián tiếp chiều cao của vật; tính khoảng cách giữa hai vị trí trong đó có một vị trí không thể tới được,...).
Theo đó, trong chương trình học môn Toán lớp 8 sẽ được học về giải thích được tính chất đường phân giác trong của tam giác, tính được độ dài đoạn thẳng bằng cách sử dụng định lí Thalès, giải quyết được một số vấn đề thực tiễn gắn với việc vận dụng định lí.
Như vậy, căn cứ quy định nêu trên thì tính chất đường phân giác được học trong chương trình môn Toán lớp 8.
Môn Toán lớp 8 có những nội dung học nào?
Căn cứ theo Mục IV Phụ lục Chương trình giáo dục phổ thông môn Toán ban hành kèm theo Thông tư 32/2018/TT-BGDĐT quy định về những nội dung học trong chương trình môn toán lớp 8 như sau:
SỐ VÀ ĐẠI SỐ
Đại số
Biểu thức đại số
Đa thức nhiều biến.
Các phép toán cộng, trừ, nhân, chia các đa thức nhiều biến
Hằng đẳng thức đáng nhớ
Phân thức đại số.
Tính chất cơ bản của phân thức đại số.
Các phép toán cộng, trừ, nhân, chia các phân thức đại số
Hàm số và đồ thị
Hàm số và đồ thị
Hàm số bậc nhất y = ax + b (a ≠ 0) và đồ thị.
Hệ số góc của đường thẳng y = ax + b (a ≠ 0).
Phương trình
Phương trình bậc nhất
HÌNH HỌC VÀ ĐO LƯỜNG
Hình học trực quan
Các hình khối trong thực tiễn Hình chóp tam giác đều, hình chóp tứ giác đều
Hình học phẳng
Định lí Pythagore
Định lí Pythagore
Tứ giác
Tứ giác
Tính chất và dấu hiệu nhận biết các tứ giác đặc biệt
Định lí Thalès trong tam giác
Định lí Thalès trong tam giác
Hình đồng dạng
Tam giác đồng dạng
Hình đồng dạng

