Vietnam: What are the properties of the angle bisector? What is the grade at which students will learn the properties of the angle bisector?

View Post in Vietnamese: >> Tính chất của đường phân giác là gì? Tính chất của đường phân giác được học ở lớp mấy?

What are the properties of the angle bisector? What is the grade at which students in Vietnam will learn the properties of the angle bisector?

In Vietnam, what are the properties of the angle bisector?

The angle bisector within a triangle has the property of dividing the angle into two equal parts and simultaneously divides the opposite side in a ratio proportional to the adjacent sides of the angle.

What are the properties of the angle bisector?

The most important property of the angle bisector:

Property: Every point located on the angle bisector of an angle is equidistant from the two sides of that angle.

Other related properties:

In a triangle: Each angle of the triangle has one and only one angle bisector.

The three angle bisectors of a triangle are concurrent at a point known as the incenter of the inscribed circle of the triangle.

In a quadrilateral: In a cyclic quadrilateral, the angle bisectors of opposite angles are perpendicular to each other.

Applications:

Geometry: Angle bisectors are widely used in problems involving triangles, quadrilaterals, and circles.

Architecture: Angle bisectors are applied in designing architectural structures, ensuring balance and harmony.

Examples:

To divide a triangular plot of land into two equal areas, the angle bisector of one angle of the triangle is often drawn.

In interior design, angle bisectors are used to divide spaces logically and symmetrically.

In summary:

The angle bisector is an important concept in geometry, with many properties and diverse applications. Understanding angle bisectors will help you better solve geometric problems and issues related to space.

*Note: Information about the properties of the angle bisector is for reference purposes only./.

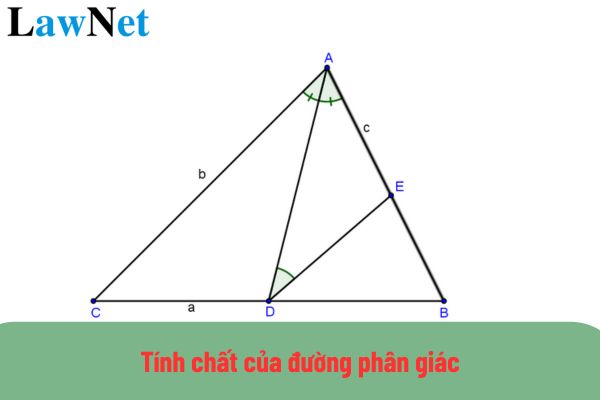
What is the Nature of the Angle Bisector? At what grade level is the nature of the angle bisector learned?

In Vietnam, what are the properties of the angle bisector? What is the grade at which students in Vietnam will learn the properties of the angle bisector? (Image from the Internet)

What is the grade at which students in Vietnam will learn the properties of the angle bisector?

Under Section IV of the Appendix of the General Education Program for Mathematics issued together with Circular 32/2018/TT-BGDDT, the learning outcomes required for the 8th-grade Mathematics curriculum are as follows:

Required learning outcomes

- Be able to explain Thales' theorem in a triangle (direct and converse theorems).

- Describe the definition of the median of a triangle. Be able to explain the properties of the median of a triangle (the median of a triangle is parallel to the third side and equal to half of it).

- Be able to explain the properties of the internal angle bisector of a triangle.

- Calculate the length of a line segment using Thales' theorem.

- Solve some practical problems by applying Thales' theorem (e.g., calculating the distance between two positions).

- Describe the definition of similar triangles.

- Explain the cases of similarity of two triangles, of two right triangles.

- Solve some practical problems by applying knowledge about similar triangles (e.g., calculate the height descent on the hypotenuse in a right triangle by using relationships between the height and the product of the two projections of the two legs on the hypotenuse; indirectly measure the height of objects; calculate the distance between two positions, one of which is unreachable, etc.).

In the 8th-grade Mathematics curriculum, students will learn the properties of the internal angle bisector of a triangle, the calculation of the length of a line segment using Thales' theorem, and the solving of some practical problems using the theorem.

Thus, under the above regulations, the properties of the angle bisector are taught in the 8th-grade Mathematics curriculum.

What are the contents of the 8th-grade Mathematics curriculum in Vietnam?

Under Section IV of the Appendix of the General Education Program for Mathematics issued with Circular 32/2018/TT-BGDDT, the contents of the 8th-grade Mathematics curriculum in Vietnam are as follows:

NUMBERS AND ALGEBRA

Algebra

Algebraic expressions

Polynomials of several variables.

Operations of addition, subtraction, multiplication, division of multivariable polynomials

Memorable identities

Algebraic fractions.

Basic properties of algebraic fractions.

Operations of addition, subtraction, multiplication, division of algebraic fractions

Functions and graphs

Linear functions y = ax + b (a ≠ 0) and their graphs.

Slope of the line y = ax + b (a ≠ 0).

Equations

Linear equations

GEOMETRY AND MEASUREMENT

Visual geometry

Shapes in practice: Equilateral triangular pyramid, equilateral quadrilateral pyramid

Plane geometry

Pythagorean theorem

Quadrilateral

Properties and signs for identifying special quadrilaterals

Thales' theorem in a triangle

Similar shapes

Similar triangles

Similar shapes

>> CLICK HERE TO READ THIS ARTICLE IN VIETNAMESE

- This translation is generated by OpenAI's GPT-4o model;

- Lawnet's response to our user's question is provided above. If you need further information, please send an email to [email protected];

- This article is for reference only;

- The regulations referred to in this article might have been annulled by the time you read it;

- For inquiries about the copyright of this article, please send an email to [email protected];

Địa chỉ:	19 Nguyễn Gia Thiều, P. Võ Thị Sáu, Q.3, TP. Hồ Chí Minh
Điện thoại:	(028) 3930 3279 (06 lines)
E-mail:	[email protected]