What is the Logarithm formula? When do students in Vietnam learn about Logarithm formula?

What is the Logarithm formula?

- The logarithm is the inverse operation of exponentiation. If a^x = b, then logₐb = x.

Where:

a: Base (must be a positive number other than 1)

x: Exponent

b: Power

*Example: log₂8 = 3, because 2³ = 8.

*Note: The information is for reference only./.

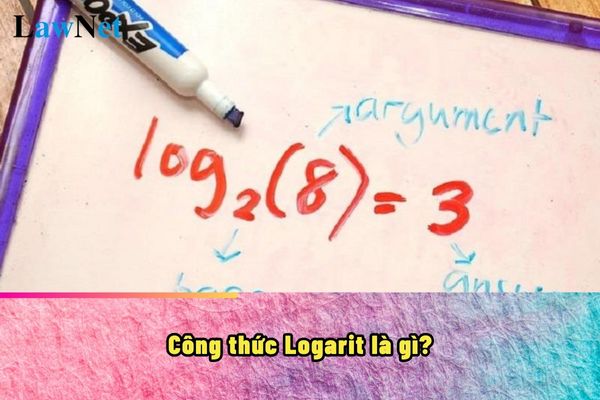
What is the Logarithm formula? When do students in Vietnam learn about Logarithm formula?​ (Image from the Internet)

When do students in Vietnam learn about Logarithm formula?

According to Section III of the General Education Program in Mathematics issued with Circular 32/2018/TT-BGDDT, the objectives for upper secondary school mathematics are as follows:

- Contributing to the formation and development of mathematical competence with the required achievements: posing and answering questions through reasoning, problem-solving; using reasoning methods, induction, and deduction to understand different ways to solve problems; establishing mathematical models to describe situations, thereby proposing solutions to the mathematical problems presented in the established models; implementing and presenting solutions to solve problems and evaluating the solutions made, reflecting the value of the solutions, generalizing similar problems; using mathematical tools and means in learning, exploring, and solving mathematical problems.

- Have basic and essential mathematical knowledge and skills about:

+ Algebra and some elements of analysis: Calculation and use of calculation tools; using algebraic language and symbols; transforming algebraic and transcendental expressions (trigonometric, exponential, logarithmic), equations, systems of equations, inequalities; recognizing basic elementary functions (power, trigonometric, exponential, logarithmic); surveying functions and drawing function graphs using derivative tools; using function language, function graphs to describe and analyze some processes and phenomena in the real world; using integrals to calculate the area of flat shapes and the volume of objects in space.

+ Geometry and Measurement: Providing knowledge and skills (at the logical reasoning level) about geometric relationships and some familiar flat shapes, spatial figures; using algebraic methods (vectors, coordinates) in geometry; developing spatial imagination; solving some practical problems associated with geometry and measurement.

+ Statistics and Probability: Enhancing the ability to collect, classify, display, analyze, and process statistical data; using statistical analysis tools through characteristic numbers measuring central tendency and dispersion for ungrouped and grouped data samples; using statistical laws in practice; recognizing random models, basic concepts of probability, and the significance of probability in practice.

- Helping students have a relatively comprehensive understanding of careers associated with mathematics and its value; providing a basis for career orientation after upper secondary school; having minimal competence to explore mathematical-related issues throughout their lifetime.

In addition, according to Section V of the General Education Program in Mathematics issued with Circular 32/2018/TT-BGDDT, the requirements for the Grade 11 mathematics program include:

- Logarithmic calculations. The properties include:

+ Recognizing the concept of logarithm base a (a > 0, a ≠ 1) of a positive real number.

+ Explaining the properties of logarithmic calculations using definitions or previously known properties.

+ Using logarithmic properties in calculating numerical expressions and simplifying expressions containing variables (written calculation and mental, quick calculations reasonably).

+ Calculating the value (exact or approximate) of logarithms using a calculator.

+ Solving some problems related to other subjects or practical issues associated with logarithmic calculations (e.g., pH problems in Chemistry,...).

- Exponential functions. Logarithmic functions include:

+ Recognizing exponential and logarithmic functions. Giving some practical examples of exponential and logarithmic functions.

+ Identifying the graphs of exponential and logarithmic functions.

+ Explaining the properties of exponential and logarithmic functions through their graphs.

+ Solving some problems related to other subjects or practical issues associated with exponential and logarithmic functions (e.g., interest rates, growth,...).

- Solving exponential and logarithmic equations and inequalities in simple forms.

>>> In summary, the logarithm formulas are taught at the upper secondary school level, specifically in the Grade 11 mathematics program.

What are the teaching methods in the Grade 11 mathematics program in Vietnam?

Moreover, according to Section VI of the General Education Program in Mathematics issued with Circular 32/2018/TT-BGDDT, the teaching methods in the Grade 11 mathematics program are as follows:

- Suitable for the student's cognitive process (from concrete to abstract, from easy to difficult); not only emphasizing the logical aspect of mathematical science but also focusing on an approach based on the students' experiences and prior knowledge.

- Adhering to the spirit of "learner-centered", promoting active, self-consciousness, paying attention to individual needs, cognitive abilities, and different learning styles of each student; organizing the teaching process towards construction, in which students participate in discovering, exploring, reasoning, and problem-solving.

- Flexibly applying active teaching methods and techniques; combining creatively and smoothly with traditional teaching methods and techniques; combining classroom learning activities with practical experiences, applying mathematical knowledge in reality. Structuring lessons to ensure a balanced proportion, harmony between core knowledge, applied knowledge, and other components.

- Fully and effectively using the minimum teaching materials and equipment as regulated for Mathematics; may use self-made teaching aids suitable for the content and student audience; enhancing the use of information technology and modern teaching tools appropriately and effectively.

- Directing teaching methods to form and develop essential qualities and common competencies.

+ Methods to form and develop essential qualities:

Through organizing learning activities, the Mathematics subject contributes along with other subjects and educational activities to help students practice honesty, love of labor, responsibility, and consciousness to complete learning tasks; nurturing self-confidence, interest in learning, the habit of reading books, and the desire to explore science.

+ Methods to form and develop common competencies:

++ Mathematics helps form and develop the ability for self-study and autonomy through training learners in selecting goals, planning their learning, forming self-study habits, reviewing, and adjusting so that they can apply these abilities in learning mathematical concepts, knowledge, and skills as well as when practicing, self-learn, or solve meaningful mathematical problems.

++ Mathematics helps form and develop communication and cooperation abilities by listening, understanding, reading, writing, and expressing necessary mathematical information in mathematical texts; efficiently using mathematical language combined with everyday language to exchange and present contents, ideas, and mathematical solutions in interactions with others, while showing confidence and respect for dialogue partners when describing and explaining mathematical contents and ideas.

++ Mathematics helps form and develop problem-solving and creativity abilities by helping students recognize problem situations; sharing the understanding of problems with others; proposing, selecting, and implementing ways and processes to solve problems and to present solutions; evaluating the solutions carried out and generalizing for similar problems.

- The method of teaching Mathematics helps form and develop computational skills, language skills, and other specific competences. To be specific:

+ Mathematics, with its outstanding advantages, has many opportunities to develop computational skills through providing mathematical knowledge, practicing calculation and estimation skills, and forming and developing the components of mathematical competence (thinking and reasoning ability, modeling ability, problem-solving ability, communication ability, and the ability to use mathematical tools).

+ Mathematics contributes to developing language skills through practicing reading comprehension, interpreting, analyzing, and evaluating mathematically meaningful situations, through efficiently using mathematical language combined with everyday language to present and explain mathematical contents, ideas, and solutions.

+ Mathematics contributes to developing information technology skills by using information technology and communication tools as supportive tools in learning and self-study; creating a learning environment for practical experiences.

+ Mathematics contributes to developing aesthetic capabilities by helping students become acquainted with the history of mathematics, the biographies of mathematicians, and recognizing the beauty of mathematics in nature.