Vietnam: What are the 2nd mid-semester question papers and answers for 10th-grade Mathematics in 2025? What are the regulations on assessing the educational outcomes for 10th-grade Mathematics?
What are the 2nd mid-semester question papers and answers for 10th-grade Mathematics in 2025?
Below are 2nd mid-semester question papers and answers for 10th-grade Mathematics in 2025:
Department of Education and Training ...
2nd mid-semester question papers for 10th-grade Mathematics in 2025
Subject: 10th-grade Mathematics
Time: 90 minutes
(excluding distribution time)
(Question paper No. 1)
I. Multiple Choice (7 points)
Question 1. Which of the following formulas does not represent y as a function of x?
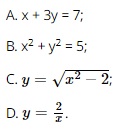
Question 2. Consider the following table of the function:
| x | 1 | 2 | 3 | 4 | 5 |
| y | 1 | 3 | 5 | 7 | 9 |
The value of the function y at x = 3 is
A. 2;
B. 3;
C. 5;
D. 7.
Question 3. Given the function y = f(x) with the graph as shown below.
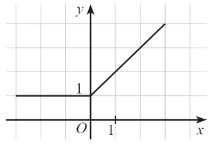
The function is increasing on the interval
A. (0; 1);
B. (1; + ∞);
C. (0; + ∞);
D. (– ∞; 0).
Question 4. The function 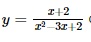 has the domain
has the domain
A. (1; 2);
B. [1; 2];
C. {1; 2};
D. ℝ \ {1; 2}.
Question 5. Given the function 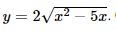 . The value of the function at x = 10 is
. The value of the function at x = 10 is

Question 6. Among the following functions, which one is not a quadratic function?
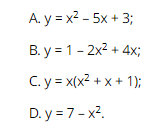
Question 7. Given the quadratic function 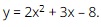 . The x-coordinate of the vertex of this quadratic function is
. The x-coordinate of the vertex of this quadratic function is

Question 8. The quadratic function 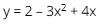 has a constant term of
has a constant term of
A. 2;
B. – 3;
C. 4;
D. – 2.
Question 9. Given the quadratic function 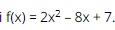 . Which of the following statements is true?
. Which of the following statements is true?
A. The function is increasing on the interval (– ∞; 2), decreasing on the interval (2; + ∞);
B. The function is increasing on the interval (– ∞; 4), decreasing on the interval (4; + ∞);
C. The function is increasing on the interval (4; + ∞), decreasing on the interval (– ∞; 4);
D. The function is increasing on the interval (2; + ∞), decreasing on the interval (– ∞; 2).
Question 10. Determine parabola 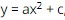 knowing that the parabola passes through two points A (1; 1) and B (2; – 2).
knowing that the parabola passes through two points A (1; 1) and B (2; – 2).
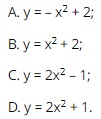
Question 11. Find the correct statement among the following statements.

Question 12. Given the function 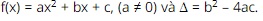 . Knowing the sign of ∆ when f(x) always has the same sign as coefficient a for all x ∈ ℝ
. Knowing the sign of ∆ when f(x) always has the same sign as coefficient a for all x ∈ ℝ
A. ∆ ≤ 0;
B. ∆ = 0;
C. ∆ > 0;
D. ∆ < 0.
Question 13. Given the quadratic expression 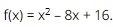 . Which of the following statements is true?
. Which of the following statements is true?
A. The equation f(x) = 0 has no solution;
B. f(x) > 0 for all x ∈ ℝ;
C. f(x) ≥ 0 for all x ∈ ℝ;
D. f(x) < 0 when x < 4.
Question 14. Among the following statements, which one is incorrect?
A. x² – 3x + 2 > 0 when x ∈ (– ∞; 1) ∪ (2; + ∞);
B. x² – 3x + 2 ≤ 0 when x ∈ [1; 2];
C. x² – 3x + 2 < 0 when x ∈ [1; 2);
D. x² – 3x + 2 ≥ 0 when x ∈ (– ∞; 1] ∪ [2; + ∞).
Question 15. The solution set of the inequality 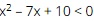
A. S = (– ∞; 2] ∪ [5; + ∞);
B. S = (– ∞; 2) ∪ (5; + ∞);
C. S = [2; 5];
D. S = (2; 5).
Question 16. Among the following statements, which one is correct?

Question 17. Among the following statements, which one is correct?
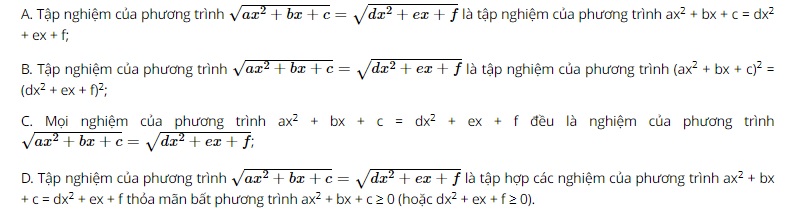
Question 18. The number of solutions of the equation 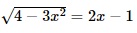
A. 0;
B. 1;
C. 2;
D. 3.
Question 19. Which of the following values is a solution of the equation 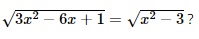 :
:
A. 2;
B. 4;
C. 12;
D. 20.
Question 20. In the coordinate plane Oxy, given the line d: 2x – y + 3 = 0. The normal vector of line d is
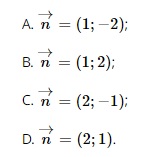
Question 21. Which point below belongs to the line d: 3x – 2y + 4 = 0?
A. A (1; 2);
B. B (0; 2);
C. C (2; 0);
D. D (2; 1).
Question 22. The parametric equation of the line ∆ passing through the point A(3; 1) and with 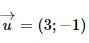 as the direction vector is:
as the direction vector is:
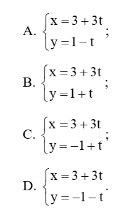
Question 23. The general equation of the line d passing through the point A (2; – 2) and with 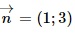 as the normal vector is
as the normal vector is
A. x – y + 2 = 0;
B. – 3x + y + 4 = 0;
C. x – 3y + 4 = 0;
D. x + 3y + 4 = 0.
Question 24. The line d has the parametric equation 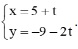 . The general equation of line d is
. The general equation of line d is
A. 2x + y – 1 = 0;
B. – 2x + y – 1 = 0;
C. x + 2y + 1 = 0;
D. 2x + 3y – 1 = 0.
Question 25. In the coordinate plane Oxy, given two points A (– 2; 3) and B (4; – 1). Which of the following equations is the equation of line AB?

Question 26. In the coordinate plane, consider the two lines

Question 27. Given the point M (x0; y0) and the line ∆: ax + by + c = 0. The distance from point M to line ∆, denoted as d (M, ∆), is calculated by the formula
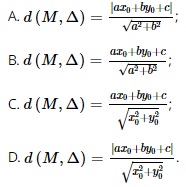
Question 28. In the coordinate plane, consider the two lines

Question 29. The distance from point A (1; 1) to the line d: 5x – 12y – 6 = 0 is
A. 13;
B. – 13;
C. – 1;
D. 1.
Question 30. The angle between two lines a: 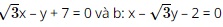 is
is
A. 30°;
B. 90°;
C. 60°;
D. 45°.
Question 31. Which of the following equations is the equation of a circle?
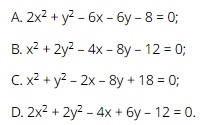
Question 32. The radius of the circle 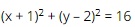 is
is
A. 16;
B. 4;
C. 256;
D. 8.
Question 33. Which of the following equations is the equation of a circle with center I (– 1; 2), radius 5?
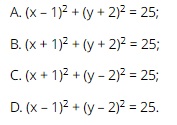
Question 34. The equation of the circle with center I(3; 4) that touches the line ∆: 3x + 4y – 10 = 0 is
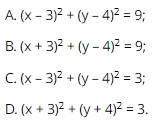
Question 35. In the coordinate plane, given the circle 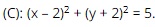 . The tangent line at point M(1; 0) on the circle (C) has the equation
. The tangent line at point M(1; 0) on the circle (C) has the equation
A. y = – 2;
B. x = 1;
C. x + 2y – 1 = 0;
D. x – 2y – 1 = 0.
II. Written Section (3 points)
Exercise 1. (1 point) Suppose the height h (unit: meters) of a golf ball over time t (unit: seconds) in one hit by an athlete is determined by a quadratic function, and the corresponding value at certain times is given by the table below:
| Time (s) | 0 | 0.5 | 1 | 2 | 3 |
| Height (m) | 0 | 28 | 48 | 64 | 48 |
a) Determine the quadratic function expressing the height h(m) of the golf ball over time t(s).
b) How long after the golfer hits the ball does it touch the ground again?

ANSWERS
I. Multiple Choice Answers Table
| 1. B | 2. C | 3. C | 4. D | 5. B | 6. C | 7. A |
| 8. A | 9. D | 10. A | 11. A | 12. D | 13. C | 14. C |
| 15. D | 16. B | 17. D | 18. B | 19. A | 20. C | 21. B |
| 22. A | 23. D | 24. A | 25. D | 26. B | 27. A | 28. C |
| 29. D | 30. A | 31. D | 32. B | 33. C | 34. A | 35. D |
II. Written Section (3 points)




Note: Information is for reference only!

What are the 2nd mid-semester question papers and answers for 10th-grade Mathematics in 2025? (Image from the Internet)
What are the regulations on assessing the educational outcomes for 10th-grade Mathematics in Vietnam?
Under Section 7 of the General education program in Mathematics issued with Circular 32/2018/TT-BGDDT:
- The assessment of the educational outcomes in Mathematics aims to provide accurate, timely, and valuable information about students' development and progress based on the requirements to be achieved in each grade and educational level; adjust teaching and learning activities to ensure each student's progress and improve the quality of Mathematics education specifically and overall education quality in general.
- Employ a variety of assessment forms (formative assessment, summative assessment) and various assessment methods (observation, documentation of execution process, oral questioning, objective testing, essay writing, written tests, practical exercises, learning projects/products, and real-world problem-solving tasks,...) at appropriate times.
- Formative assessment (or continuous assessment) is organized by the subject teacher, combined with assessments by teachers of other subjects, self-assessment by the student being assessed, and by other students in the group, class, or assessment by parents.
Formative assessment accompanies the student's learning activities, avoiding separation between teaching and assessment processes, ensuring the assessment targets student learning progress.
- Summative assessment mainly aims to evaluate the achievement of learning objectives.
Summative assessment results are used to certify learning levels and recognize student achievements.
Periodic assessments are organized by educational institutions or through national exams and assessments.
- Periodic assessments are also used to manage teaching activities to ensure quality at educational institutions and serve the development of the Mathematics curriculum.
- Assessing student competencies through evidence of outcomes achieved during their action processes.
The assessment process includes basic steps such as: defining assessment purposes; determining necessary evidence; selecting appropriate assessment methods and tools; collecting evidence; interpreting the evidence and making comments.
- Emphasize choosing assessment methods and tools for components of mathematical competence. To be specific::
+ Assess mathematical thinking and reasoning competence: utilize assessment methods and tools such as questions (oral, written), exercises,... that require students to present, compare, analyze, aggregate, and systematize knowledge;
Apply mathematical knowledge to explain and reason.
+ Assess mathematical modeling competence: select practical situations that give rise to mathematical problems.
From there, students must identify a mathematical model (including formulas, equations, charts, graphs,...) for the situation emerging in the practical problem;
Solve mathematical issues within the established model; present and evaluate solutions in practical contexts and improve the model if problem-solving approaches are unsuitable.
+ Assess problem-solving competence in mathematics: use methods such as requiring learners to identify situations, discover, and present issues to be resolved;
Describe and explain initial information, goals, and expectations of the problem situation under consideration; collect, select, arrange information, and connect with existing knowledge;
Use questions (which may require oral or written responses) that require learners to apply knowledge to solve problems, particularly practical issues; use observation methods (like checklists according to predefined criteria), and observe learners during problem-solving;
Assess through learners' practical products (such as learning project outputs); reasonably consider integrated assessment tasks.
+ Assess mathematical communication competence: use methods such as requiring learners to listen, read, note (summarize), analyze, select, and extract basic, focal mathematical information in spoken or written texts;
Utilize mathematical language combined with ordinary language in presenting, expressing, questioning, discussing, and debating mathematical content, ideas, and solutions in interaction with others.
+ Assess the competence to use mathematical tools and means: use methods such as requiring learners to recognize the names, functions, usage specifications, maintenance methods, advantages, and limitations of mathematical tools and means;
Present appropriate usage of mathematical tools and means to perform learning tasks or to describe mathematical arguments and proofs.
When planning lessons, teachers should establish criteria and assessment methods to ensure that by the end of each lesson, students achieve basic requirements based on stated criteria before proceeding to subsequent learning activities.
What are the general objectives of learning 10th-grade Mathematics in Vietnam?
Under Section 3 of the General education program in Mathematics in the general education program, issued with Circular 32/2018/TT-BGDDT, the general objectives of learning 10th-grade Mathematics in Vietnam are as follows:
- The Mathematics curriculum helps students achieve the following main goals:
+ Form and develop mathematical competence, including the following core components: mathematical thinking and reasoning competence; mathematical modeling competence; problem-solving competence in mathematics; mathematical communication competence; and competence in using mathematical tools and means.
+ Contribute to forming and developing in students essential qualities and general competencies according to levels suitable for the subject and educational level as stipulated in the overall curriculum.
+ Gain basic, essential general mathematics knowledge and skills; develop problem-solving capacities that integrate multiple disciplines, including Mathematics and other subjects such as Physics, Chemistry, Biology, Geography, Informatics, Technology, History, and Arts,...; create opportunities for students to experience and apply mathematics in practical situations.
+ Have a relatively comprehensive understanding of the usefulness of mathematics to related careers, providing a foundation for career orientation, as well as sufficient minimal competence to independently seek out mathematics-related issues throughout life.

