Guidelines for grade 6 Math in Vietnam: How to calculate the area of a rhombus?
Guidelines for grade 6 Math in Vietnam: How to calculate the area of a rhombus?
A rhombus is a quadrilateral with four equal sides or a parallelogram with two perpendicular diagonals that bisect each other at their midpoints.
There are different methods to calculate the area of a rhombus depending on the specific type of exercise:
1. Given the Lengths of Two Diagonals
When the lengths of the two diagonals of the rhombus are given, the area of the rhombus is half the product of the lengths of the two diagonals. The formula for calculating the area of the rhombus in this case is:
S = 1/2 x (d1 x d2)
Where: S is the area of the rhombus, d1 is the length of diagonal d1, and d2 is the length of diagonal d2.
2. Given the Height and the Base of the Rhombus
In this case, to calculate the area of the rhombus, we need to use the base and the height of the rhombus.
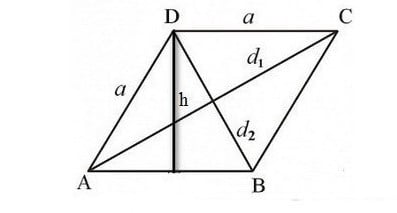
The formula for calculating the area of the rhombus using the base and the height is:
S = h x a
Where: S is the area of the rhombus, h is the height of the rhombus, and a is the base.
Example: Given a rhombus with sides AB = CD = BC = DA = 6cm and the height of the rhombus is 3cm. Apply the rhombus area formulas to solve the exercise.
Solution: S = h x a = 3 x 6 = 18 cm²
3. Calculating the Area of the Rhombus Based on a Triangle's Trigonometric Formula
This method is used when the exercise provides the measure of an angle of the rhombus. The formula for calculating the area of the rhombus in this case is:
S = ½ x a x b x sin(C)
Where: a and b are two sides of the triangle, and C is the angle between these two sides.
| Exercises for Calculating the Area of the Rhombus Exercise 1: A piece of land in the shape of a rhombus has the sum of the lengths of its diagonals as 400 cm. Knowing that the length of the first diagonal is 3/5 of the length of the second diagonal, calculate the area of the rhombus. Solution: The total number of equal parts is: 3 + 5 = 8 (parts) The length of the second diagonal is: 400 : 8 x 5 = 250 (cm) The length of the first diagonal is: 400 - 250 = 150 (cm) The area of the rhombus is: 250 x 150 : 2 = 18750 (cm²) Answer: 18750 cm² Exercise 2: Given a rhombus ABCD where O is the intersection of the two diagonals. The area of the rhombus is known to be 60 cm², and AC = 10 cm. Calculate the length of the side of the rhombus. Solution: The area of the rhombus is: S = 1/2 . AC . BD ⇒ BD = (2.S)/AC = (2 . 60) / 10 = 12 (cm) According to the properties of the rhombus, O is the midpoint of both AC and BD. Thus: OA = 1/2 . AC = 1/2 . 10 = 5 (cm) and OB = 1/2 . BD = 1/2 . 12 = 6 (cm) By applying the Pythagorean theorem in triangle AOB, we have: AB² = OA² + OB² = 5² + 6² = 61, hence: AB = 7.81 (cm) Therefore, the length of the side of the rhombus is: 7.81 cm Exercise 3: A piece of land in the shape of a rhombus has diagonals measuring 70m and 300m. Calculate the area of this piece of land. Solution: The area of the land is: (70 × 300) : 2 = 10500 (m²) Answer: 10500 m² Exercise 4: A rhombus has the sum of the lengths of its diagonals as 45cm, knowing that the first diagonal is 3/2 of the length of the second diagonal. What is the area of this rhombus? Solution: The total number of equal parts: 3 + 2 = 5 (parts) The length of the first diagonal is: 45 : 5 x 3 = 27 (cm) The length of the second diagonal is: 45 - 27 = 18 (cm) The area of the rhombus: 27 x 18 : 2 = 243 (cm²) Answer: 243 cm². Exercise 5: A piece of land in the shape of a rhombus has each side measuring 42m. The land needs to be fenced with 4 strands of barbed wire. How many meters of barbed wire are required for the fencing? Solution: The circumference of the rhombus: 42 x 4 = 168 (m) The total length of barbed wire needed for fencing the land is: 168 x 4 = 672 (m) Answer: 672 m. |
Guidelines for grade 6 Math in Vietnam: How to calculate the area of a rhombus? (Image from the Internet)
What is the content of geometry and measurement in grade 6 Math program in Vietnam?
Based on the Mathematics Curriculum for the General Education Program issued under Circular 32/2018/TT-BGDDT, the content of geometry and measurement in grade 6 includes 2 parts:
I. Visual Geometry
1. Plane figures in practice
- Equilateral triangle, square, regular hexagon
- Rectangle, rhombus, parallelogram, isosceles trapezoid
2. Symmetry of plane figures in the natural world
- Figures with axis symmetry
- Figures with point symmetry
- The role of symmetry in the natural world
II. Plane Geometry
1. Basic geometric figures
- Point, line, ray
- Line segment, length of a line segment
- Angle, special angles, angle measure
What is the duration of the grade 6 Math program in Vietnam?
According to the General Education Program for mathematics issued under Circular 32/2018/TT-BGDDT:
| Grade | Grade 1 | Grade 2 | Grade 3 | Grade 4 | Grade 5 | Grade 6 | Grade 7 | Grade 8 | Grade 9 | Grade 10 | Grade 11 | Grade 12 |
| Number of periods | 105 | 175 | 175 | 175 | 175 | 140 | 140 | 140 | 140 | 105 | 105 | 105 |
Thus, the duration of the grade 6 mathematics program is 140 periods.

